Dynamic networks
The dynamic networks that we consider in this app and toolbox can be twofold:
- Directed (module) dynamic networks, and
- Undirected (diffusively coupled) dynamic networks
While the first category is mainly described by interconnected rational transfer function matrices, the second category is more strongly based on underlying physical equations, and represented by polynomial matrices.
Module dynamic networks
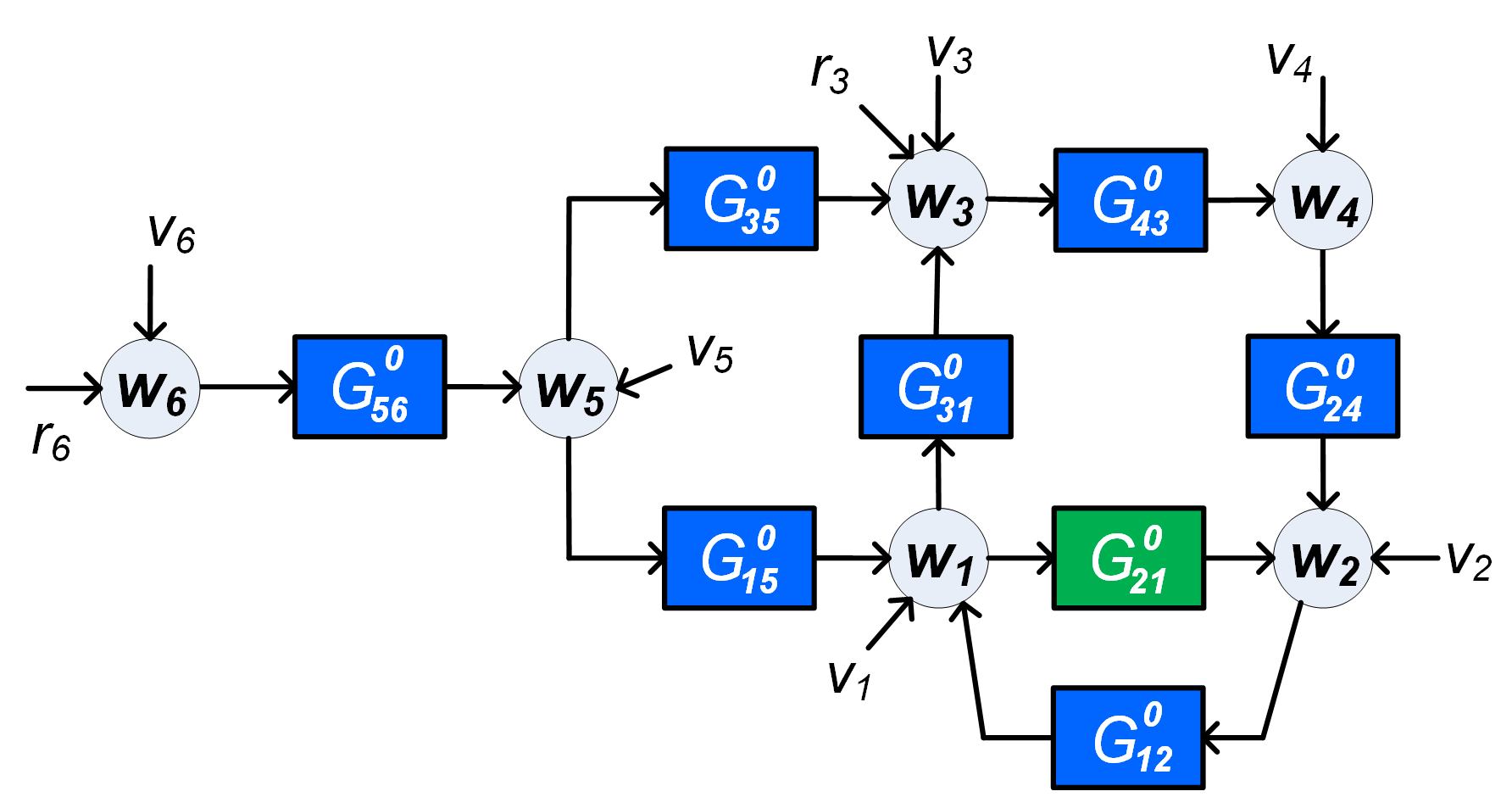
Module dynamic networks are directed networks, where network components (modules) are linear time-invariant (single input, single output) dynamic systems that appear on the links in a graph, connecting nodes that represent node signals as time series.
A module dynamic network is characterized by the equation (in discrete-time)
with:
- : a column vector of internal node variables, , each being a time series;
- : the discrete-time variable;
- : a vector of external excitation variables;
- : a vector of white noise (disturbance) variables;
- : the dynamic network matrix; a rational matrix indicating which node gets input from which other nodes in the network;
- : a dynamic transfer matrix, representing the mapping from external excitation variables to internal node variables;
- : a dynamic transfer matrix, modeling the disturbances that are present on the node variables.
- : the time-shift variable, ;
The topology of the network, i.e. its interconnectionm structure, is reflected in binary adjacency matrices representing the structural properties of , indicating which link/module is present (=1) or not (=0). There is a link from node to node if in the adjacency matrix of element equals .
External signals , if present, are typically available to the user, together with a selection of node variables in .
Example of an identification problem in dynamic networks:
- For a given topology, evaluate under which conditions on the presence/measurability of and signals, we can estimate the dynamics of a module or of the full network.
Reference:
- P.M.J. Van den Hof, A. Dankers, P. Heuberger and X. Bombois (2013). Identification of dynamic models in complex networks with prediction error methods - basic methods for consistent module estimates. Automatica, Vol. 49, no. 10, pp. 2994-3006.
Diffusively coupled dynamic networks

Diffusively coupled dynamic networks are undirected networks, represented by coupled linear differential (difference) equations, that interconnect nodes that represent node signals as time series. The links in the graph are represented by polynomials in the differential (difference) operator. The network includes connections to a ground node.
A diffusively coupled network is characterized by the equation (in discrete-time)
with:
- : a column vector of internal node variables, , each being a time series;
- : the discrete-time variable;
- : a vector of external excitation variables;
- : a vector of white noise (disturbance) variables;
- : the dynamic network matrix; a symmetric polynomial matrix indicating which node gets input from which other nodes in the network;
- : a dynamic polynomial matrix, representing the mapping from external excitation variables to internal node variables;
- : a dynamic (rational) transfer matrix, modeling the disturbances that are present on the node variables.
- : the time-shift variable, ;
The topology of the network, i.e. its interconnectionm structure, is reflected in binary adjacency matrices representing the structural properties of , indicating which link/module is present (=1) or not (=0). There is a link from node to node if in the adjacency matrix of element equals .
The symmetric network matrix can uniquely be decomposed into:
with being diagonal and a Laplacian matrix, where:
- the terms represent the connection of node to the ground, and
- the terms represent the interconnection between nodes and .
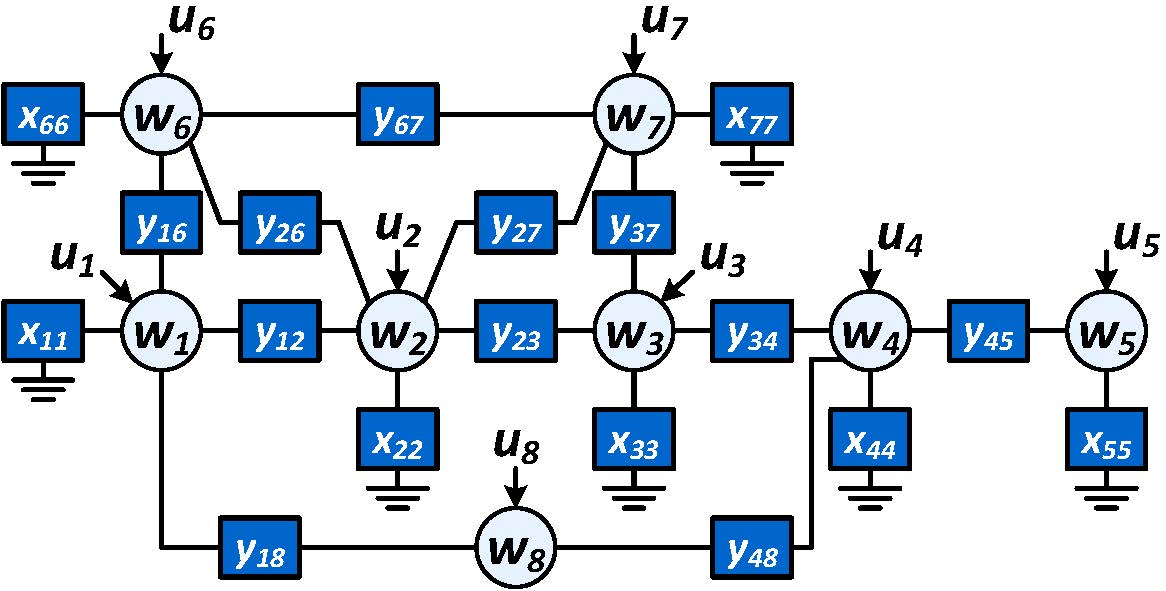
External signals , if present, are typically available to the user, together with a selection of node variables in .
Reference:
- E.M.M. Kivits and P.M.J. Van den Hof (2022). Identification of diffusively coupled linear networks through structured polynomial models. IEEE Trans. Automatic Control, Vol. 68, no. 6, pp. 3513-3528, June 2023.
- E.M.M. Kivits (2024). Modelling and Identification of Physical Linear Networks. PhD Thesis, Eindhoven University of Technology, February 2024.